Correlation Analysis
Introduction
Correlation is the statistical tool which is used to know the relationship between two or more variables i.e. the degree to which the variables are associated with each other. In simpler words, it measures the closeness of the relationship. For example, price and supply, demand and supply, income and expenditure are correlated.
Suppose in a manufacturing firm, they want to know the relation between production volume & the efficiency of machinery equipment. In this case, we can use correlation analysis.
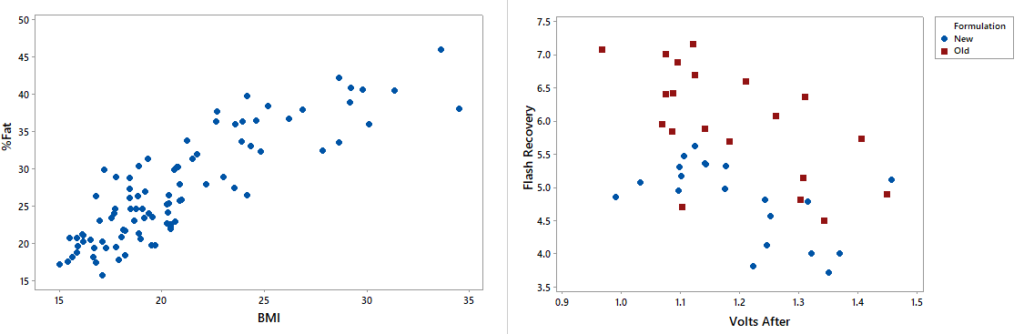
What are types of correlation?
- Positive Correlation – When the variables are changing in the same direction (either increase or decrease in parallel), we call it as a positively correlated. For e.g. price of a goods and demand, hot weather and cold drink consumptions, etc.
- Negative Correlation – When the variables are changing in the opposite direction (One is increasing and other is decreasing), we call it as a negatively correlated. For e.g. alcohol consumption and lifeline, smartphones usages and battery lifeline, etc.
- Zero Correlation – We call it a zero correlated when there is no relationship between the variables (Correlation=0). For e.g. HR recruits and temperature, paper production and beverages, etc.
When we want to know relationship between the variables in any kind of scenarios – What we do first? Our answer would be we collect the data first and to make it visualize properly. We plot it on scatterplot. We can state that it is a simple diagrammatic study to examine the correlation between the factors.
Scatter plot is a simple graph where the data of two continuous variables are plotted against each other. The data values are plotted in the form of dots. It examines the relationship between two variables and to check the degree of association between them. One variable is called the independent variable and the other variable is called the dependent variable. The degree of association of a variable is known as correlation.
Suppose in a glass manufacturing industry scenario, we want to know whether the temperature and chemical formulation is related or not. We want to check the relation – “How strong or weak it is?” It helps to identify the strength of the relationship between two factors and their cause and effect relationship. It is the fundamental tool in correlation and regression analysis.
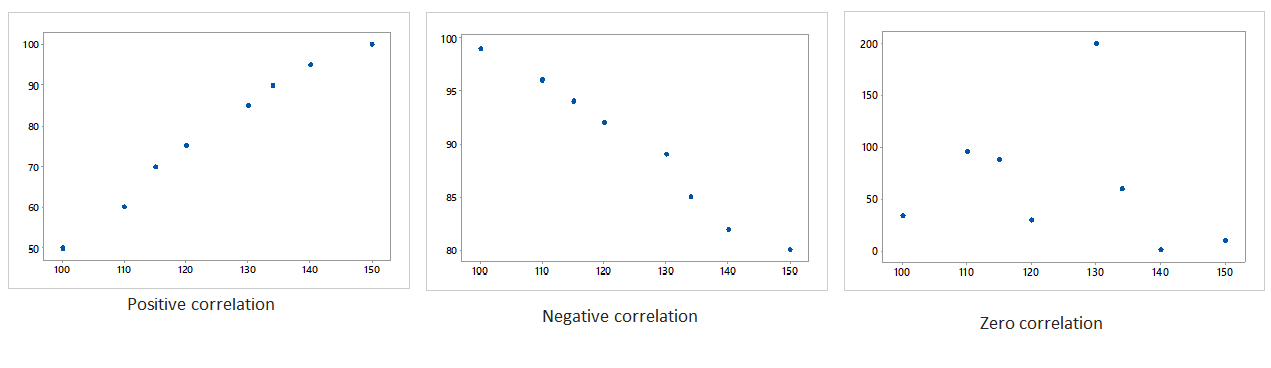Generally three types of correlation are mentioned above using a scatterplots. A positive correlation is a type of correlation between two variables when both the variables are changes in same direction. When one keeps increasing and the other keeps increasing too. A negative correlation is a contradiction to positive correlation. It means as one variable increases and the other decreases. When there is no relationship between the variables and all the data points are scattered everywhere. In such case there is no correlation.
- Data are numerical in nature.
- To check the cause and effect relationships between the pair of continuous variables.
- To identify the outlier in a process.
- To examine whether there is a relationship exists between the variables.
- Easy visualization of the data variables or factors.
- Plotting the graph is relatively simple.
- To track the patterns or trends of a data.
- Best used for the optimization of a process.
It is measure by the correlation coefficient (r) – which is a statistical measure of the degree, to which change to the value of one variable varies change to the value of another.
Correlation methods
- Karl Pearson’s Coefficient of Correlation – It is widely used to find correlation of a numeric variables. To find the relationship between two variables ( Say x and y), we can use the formula.
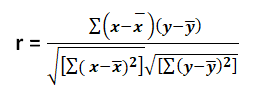For e.g. in an automobile manufacturing industry, we can check the relationship between weight and mileage of a cars. We will take weight of cars (x) and mileage of cars (y). After finding mean of x and y, equate on the above formula and we get r=0.73. This means the weight and mileage of care are positively correlated.
- Spearman’s Rank Correlation Coefficient – It is used to study the degree of association between the ranked variables. To find the relationship between two variables ( Say X and Y), we can use the formula
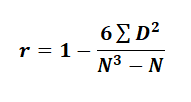For e.g. in the steel industry, a manufacturer wants to find a relation between material and labour costs based on expenditure. Now, we will rank it according to the cost (Say R1. for material & R2. for labour) and subtract it (We will get D). After equating those values on the above formula, we get r=0.89. This means the relationship between materials and labour is highly positively correlated based on expenditure.
Some important interpretations
- Value of correlation coefficient ‘r’ ranges from -1 to +1.
- If r = +1, then the correlation between the two variables is said to be perfect and positive.
- If r = -1, then the correlation between the two variables is said to be perfect and negative.
- If r = 0, then there exists no correlation between the variables.
Attend our Training Program, to know more about Statistics and Statistical Software. We conduct various training programs – Statistical Training and Minitab Software Training. Some of the Statistical training certified courses are Predictive Analytics Masterclass, Essential Statistics For Business Analytics, SPC Masterclass, DOE Masterclass, etc. (Basic to Advanced Level). Some of the Minitab software training certified courses are Minitab Essentials, Statistical Tools for Pharmaceuticals, Statistical Quality Analysis & Factorial Designs, etc. (Basic to Advanced Level).
We also provide a wide range of Business Analytics Solutions and Business Consulting Services for Organisations to make data-driven decisions and thus enhance their decision support systems.