Regression Analysis
Introduction
Suppose we want to estimate growth in sales of a company based on current status. We have the past company data which indicates that the growth in sales is around one and a half times the growth in the economy. Using this insight, we can do regression analysis and predict future sales of the company.
For example,
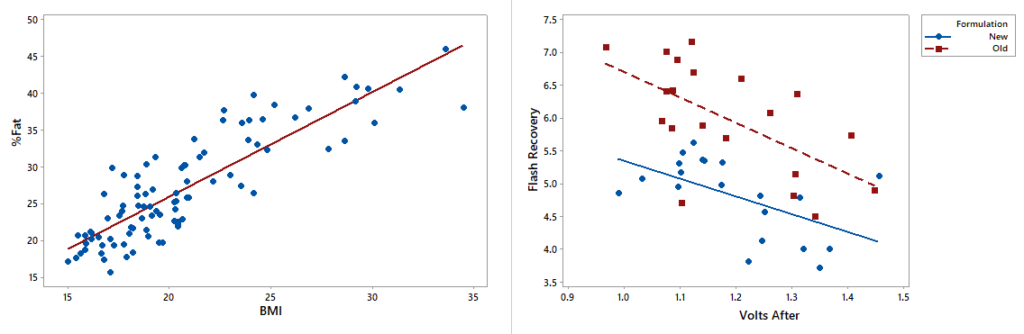
- How does processing temperature relate to the mean hardness of steel?
- How hard can you expect the tablets to be when processed at a particular temperature for a certain amount of time?
- Does adding more copper to an alloy always make it stronger, or does strength decrease at higher concentrations?
What is Regression Analysis?
Regression analysis is a powerful technique in the field of statistical analysis used in prediction of the value of an unknown variable from a known variable, in predicting the value of one variable, given the value of another variable, when those variables are correlated to each other. Basically, regression analysis is used to predict an outcome based on historical data. It is also called a predictive analysis.
Before going to the types of regression analysis, let us first understand the basic of Regression Equation. The relationship between variables in a regression analysis is expressed by an equation known as regression equation.
Now, let’s discuss the types of regression
- Simple Linear regression – It is used to study the linear relationship between one independent and one dependent variable. This analysis assumes that there is a linear association between the two variables. Regression equation is given by
![]() where,
where,
- x – Independent variable
- y – Dependent variable
- βo – y intercept point
- β1 – Slope of the line (Regression coefficient)
- Multiple Linear regressions – It is used to study the linear relationship between one dependent variable and more than two independent variables. This analysis assumes that there is a linear association between the variables. Regression equation is given by
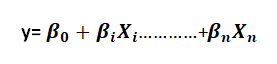
where,
- 𝑿𝒊 𝑡𝑜 𝑿𝒏 – independent variable
- y – Dependent variable
- βo – y Intercept point
- β1 – Regression coefficient of variable 𝒙𝟏
- 𝛽2 – Regression coefficient of variable 𝒙𝟐
Reference –
- Independent variable (x) – Also known as a predictor or explanatory variables. It is used to predict or to explain the behaviour of the dependent variable.
- Dependent variable (y) – Also known as Response or Output variable. This is the variable that we are trying to understand or predict and depends on the values of independent variables.
Suppose in an automobile manufacturing industry, let us check the relationship between weight and mileage of a cars
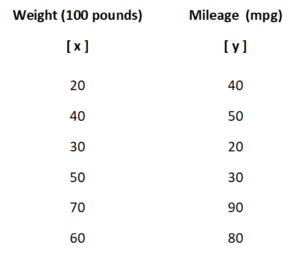
Here,
- x – Independent variable & y – Dependent variable
- First, we will fit the data in a scatterplot with regression line to check whether it is a linear or nonlinear regression equation.
- Then equate on a Regression Equation
![]()
where,
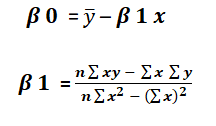
- After equating all the values on a Regression equation,
![]()
- From the resultant equation, we can predict the value of Y based on x as x is an independent variable.
With reference to above example, we will add one more independent variable i.e. fuel capacity

Here,
- x1 & x2 – Independent variables & y – Dependent variable
- First, we will fit the data in a scatterplot matrix with regression line to check whether it is a linear or nonlinear regression equation.
- Then equate on a Regression Equation
![]()
where,
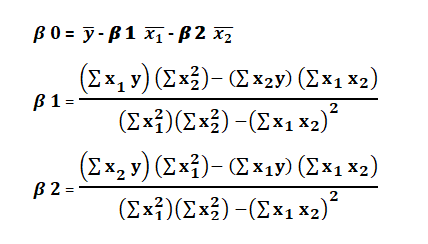
- After equating all the values on a Regression equation,
![]()
- From the resultant equation, we can predict the value of y based on x1 & x2 (independent variables).
Attend our Training Program, to know more about Statistics and Statistical Software. We conduct various training programs – Statistical Training and Minitab Software Training. Some of the Statistical training certified courses are Predictive Analytics Masterclass, Essential Statistics For Business Analytics, SPC Masterclass, DOE Masterclass, etc. (Basic to Advanced Level). Some of the Minitab software training certified courses are Minitab Essentials, Statistical Tools for Pharmaceuticals, Statistical Quality Analysis & Factorial Designs, etc. (Basic to Advanced Level).
We also provide a wide range of Business Analytics Solutions and Business Consulting Services for Organisations to make data-driven decisions and thus enhance their decision support systems.